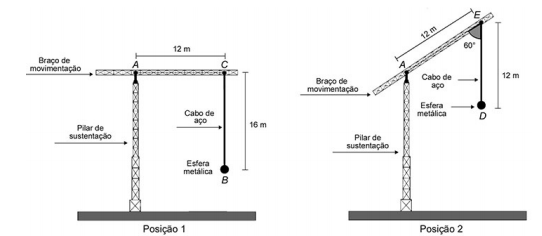
cód. #75210
INEP - Matemática - 2021 - Exame Nacional do Ensino Médio - Primeiro Dia e Segundo Dia - Digital
O ganho real de um salário, r, é a taxa de crescimento do poder de compra desse salário. Ele é calculado a partir do percentual de aumento dos salários e da taxa de inflação, referidos a um mesmo período. Algebricamente, pode-se calcular o ganho real pela fórmula
1 + r = 1+i / 1+f,
em que i é o percentual de aumento no valor dos salários e f é a taxa de inflação, ambos referidos a um mesmo período.
Considere que uma categoria de trabalhadores recebeu uma proposta de aumento salarial de 10%, e que a taxa de inflação do período correspondente tenha sido 5%. Para avaliar a proposta, os trabalhadores criaram uma classificação em função dos ganhos reais conforme o quadro.
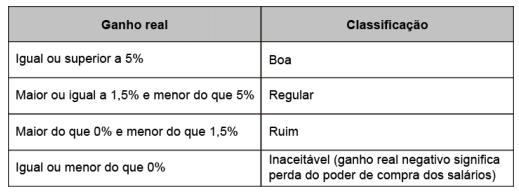
Eles classificaram a proposta de aumento e justificaram essa classificação apresentando o valor do ganho real que obteriam.
A classificação, com sua respectiva justificativa, foi
A) inaceitável, porque o ganho real seria mais próximo de – 5%.
B) ruim, porque o ganho real seria mais próximo de 1,05%.
C) regular, porque o ganho real seria mais próximo de 4,7%.
D) boa, porque o ganho real seria mais próximo de 9,5%.
E) boa, porque o ganho real seria mais próximo de 5%.
A
B
C
D
E