cód. #75229
INEP - Matemática - 2021 - Exame Nacional do Ensino Médio - Primeiro Dia e Segundo Dia - Digital
O Índice de Desenvolvimento da Educação Básica (Ideb), criado para medir a qualidade do aprendizado do ensino básico no Brasil, é calculado a cada dois anos. No seu cálculo são combinados dois indicadores: o aprendizado e o fluxo escolar, obtidos a partir do Censo Escolar e das avaliações oficiais promovidas pelo Inep.
O Ideb de uma escola numa dada série escolar pode ser calculado pela expressão
Ideb = N x P,
em que N é a média da proficiência em língua portuguesa e matemática, obtida a partir do Sistema de Avaliação da Educação Básica (Saeb), e variando de 0 a 10. O indicador P, que varia de 0 a 1, por sua vez, refere-se ao fluxo escolar, pois considera as taxas de aprovação e reprovação da instituição, sendo calculado por
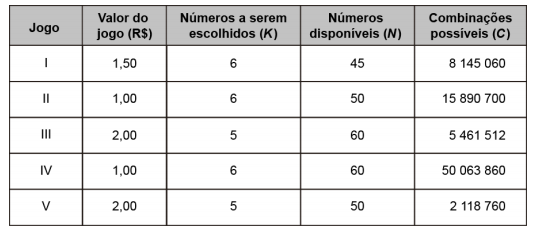
P = 1/T,
em que T é o tempo médio de permanência dos alunos na série.
Disponível em: www.inep.gov.br. Acesso em: 2 ago. 2012.
Uma escola apresentou no 9º ano do ensino fundamental, em 2017, um Ideb diferente daquele que havia apresentado nessa mesma série em 2015, pois o tempo médio de permanência dos alunos no 9º ano diminuiu 2%, enquanto a média de proficiência em língua portuguesa e matemática, nessa série, aumentou em 2%.
Dessa forma, o Ideb do 9º ano do ensino fundamental dessa escola em 2017, em relação ao calculado em 2015,
A) permaneceu inalterado, pois o aumento e a diminuição de 2% nos dois parâmetros anulam-se.
B) aumentou em 4%, pois o aumento de 2% na média da proficiência soma-se à diminuição de 2% no tempo médio de permanência dos alunos na série.
C) diminuiu em 4,04%, pois tanto o decrescimento do tempo médio de permanência dos alunos na série em 2% quanto o crescimento da média da proficiência em 2% implicam dois decréscimos consecutivos de 2% no valor do Ideb.
D) aumentou em 4,04%, pois tanto o decrescimento do tempo médio de permanência dos alunos na série em 2% quanto o crescimento da média da proficiência em 2% implicam dois acréscimos consecutivos de 2% no valor do Ideb.
E) aumentou em 4,08%, pois houve um acréscimo de 2% num parâmetro que é diretamente proporcional e um decréscimo de 2% num parâmetro que é inversamente proporcional ao Ideb.
A
B
C
D
E



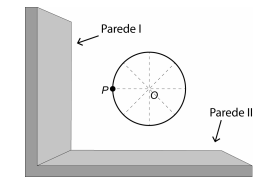 O brinquedo está situado nas proximidades de duas paredes verticais e perpendiculares entre si. Seja
O brinquedo está situado nas proximidades de duas paredes verticais e perpendiculares entre si. Seja