Questões de Matemática do ENEM

Os tempos gastos por três alunos para resolver um mesmo exercício de matemática foram: 3,25 minutos; 3,4 minutos e 191 segundos.

O tempo gasto a mais, em segundo, pelo aluno que concluiu por último a resolução do exercício, em relação ao primeiro que o finalizou, foi igual a

O gráfico apresenta a evolução do crescimento de uma determinada árvore, plantada a partir de uma muda com 1 metro de altura. Nessa evolução, a altura da árvore, em metro, é descrita em função do tempo, medido em ano.

No período de 1 ano, contado a partir do instante em que a árvore tinha dois anos e meio de plantio, a variação da altura dessa árvore, em metro, teve valor compreendido entre

Em um país, as infrações de trânsito são classificadas de acordo com sua gravidade. Infrações dos tipos leves e médias acrescentam, respectivamente, 3 e 4 pontos na carteira de habilitação do infrator, além de multas a serem pagas. Um motorista cometeu 5 infrações de trânsito. Em consequência teve 17 pontos acrescentados em sua carteira de habilitação.

Qual é a razão entre o número de infrações do tipo leve e o número de infrações do tipo média cometidas por esse motorista?

Na última eleição para a presidência de um clube, duas chapas se inscreveram (I e II). Há dois tipos de sócio: patrimoniais e contribuintes. Votos de sócios patrimoniais têm peso 0,6 e de sócios contribuintes têm peso 0,4. A chapa I recebeu 850 votos de sócios patrimoniais e 4 300 de sócios contribuintes; a chapa II recebeu 1 300 votos de sócios patrimoniais e 2 120 de sócios contribuintes. Não houve abstenções, votos em branco ou nulos, e a chapa I foi vencedora. Haverá uma nova eleição para a presidência do clube, com o mesmo número e tipos de sócios, e as mesmas chapas da eleição anterior. Uma consulta feita pela chapa II mostrou que os sócios patrimoniais não mudarão seus votos, e que pode contar com os votos dos sócios contribuintes da última eleição. Assim, para que vença, será necessária uma campanha junto aos sócios contribuintes com o objetivo de que mudem seus votos para a chapa II.

A menor quantidade de sócios contribuintes que precisam trocar seu voto da chapa I para a chapa II para que esta seja vencedora é

Um grupo de engenheiros está projetando um motor cujo esquema de deslocamento vertical do pistão dentro da câmara de combustão está representado na figura.

A função h(t) = 4 + 4sen (βt /2 - π/2) definida para t ≥ 0 descreve como varia a altura h, medida em centímetro, da parte superior do pistão dentro da câmara de combustão, em função do tempo t, medido em segundo. Nas figuras estão indicadas as alturas do pistão em dois instantes distintos.

O valor do parâmetro β , que é dado por um número inteiro positivo, está relacionado com a velocidade de deslocamento do pistão. Para que o motor tenha uma boa potência, é necessário e suficiente que, em menos de 4 segundos após o início do funcionamento (instante t = 0), a altura da base do pistão alcance por três vezes o valor de 6 cm. Para os cálculos, utilize 3 como aproximação para π.

O menor valor inteiro a ser atribuído ao parâmetro β , de forma que o motor a ser construído tenha boa potência, é

Para construir uma piscina, cuja área total da superfície interna é igual a 40 m², uma construtora apresentou o seguinte orçamento:

• R$ 10 000,00 pela elaboração do projeto;

• R$ 40 000,00 pelos custos fixos;

• R$ 2 500,00 por metro quadrado para construção da área interna da piscina.

Após a apresentação do orçamento, essa empresa decidiu reduzir o valor de elaboração do projeto em 50%, mas recalculou o valor do metro quadrado para a construção da área interna da piscina, concluindo haver a necessidade de aumentá-lo em 25%. Além disso, a construtora pretende dar um desconto nos custos fixos, de maneira que o novo valor do orçamento seja reduzido em 10% em relação ao total inicial.

O percentual de desconto que a construtora deverá conceder nos custos fixos é de

Uma construtora pretende conectar um reservatório central (R_c) em formato de um cilindro, com raio interno igual a 2 m e altura interna igual a 3,30 m, a quatro reservatórios cilíndricos auxiliares (R₁, R₂, R₃ e R₄), os quais possuem raios internos e alturas internas medindo 1,5 m.

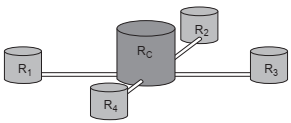
As ligações entre o reservatório central e os auxiliares são feitas por canos cilíndricos com 0,10 m de diâmetro interno e 20 m de comprimento, conectados próximos às bases de cada reservatório. Na conexão de cada um desses canos com o reservatório central há registros que liberam ou interrompem o fluxo de água.

No momento em que o reservatório central está cheio e os auxiliares estão vazios, abrem-se os quatro registros e, após algum tempo, as alturas das colunas de água nos reservatórios se igualam, assim que cessa o fluxo de água entre eles, pelo princípio dos vasos comunicantes.

A medida, em metro, das alturas das colunas de água nos reservatórios auxiliares, após cessar o fluxo de água entre eles, é

A taxa de urbanização de um município é dada pela razão entre a população urbana e a população total do município (isto é, a soma das populações rural e urbana). Os gráficos apresentam, respectivamente, a população urbana e a população rural de cinco municípios (I, II, III, IV, V) de uma mesma região estadual. Em reunião entre o governo do estado e os prefeitos desses municípios, ficou acordado que o município com maior taxa de urbanização receberá um investimento extra em infraestrutura.

Segundo o acordo, qual município receberá o investimento extra?

Em um determinado ano, os computadores da receita federal de um país identificaram como inconsistentes 20% das declarações de imposto de renda que lhe foram encaminhadas. Uma declaração é classificada como inconsistente quando apresenta algum tipo de erro ou conflito nas informações prestadas. Essas declarações consideradas inconsistentes foram analisadas pelos auditores, que constataram que 25% delas eram fraudulentas. Constatou-se ainda que, dentre as declarações que não apresentaram inconsistências, 6,25% eram fraudulentas.

Qual é a probabilidade de, nesse ano, a declaração de um contribuinte ser considerada inconsistente, dado que ela era fraudulenta?

Um comerciante, que vende somente pastel, refrigerante em lata e caldo de cana em copos, fez um levantamento das vendas realizadas durante a semana. O resultado desse levantamento está apresentado no gráfico.

Ele estima que venderá, em cada dia da próxima semana, uma quantidade de refrigerante em lata igual à soma das quantidades de refrigerante em lata e caldo de cana em copos vendidas no respectivo dia da última semana. Quanto aos pastéis, estima vender, a cada dia da próxima semana, uma quantidade igual à quantidade de refrigerante em lata que prevê vender em tal dia. Já para o número de caldo de cana em copos, estima que as vendas diárias serão iguais às da última semana.

Segundo essas estimativas, a quantidade a mais de pastéis que esse comerciante deve vender na próxima semana é